AI for Dummies

Nu we begrijpen hoe machines leren, gaan we kijken naar de kernalgoritmes die dit allemaal mogelijk maken. Hoewel er honderden verschillende machine learning-technieken bestaan, vallen de meeste in twee fundamentele categorieën op basis van het soort output dat ze produceren.

Regression-algoritmes voorspellen continue numerieke waarden—zoals het schatten van huizenprijzen, het voorspellen van temperaturen of het berekenen van aandelenrendement. Classification-algoritmes delen data in categorieën—zoals het identificeren van spam, het stellen van diagnoses of het herkennen van objecten op foto’s.

Regression: Nummers Voorspellen

Regression-modellen blinken uit in het voorspellen van continue waarden waarbij de output elk getal binnen een bereik kan zijn. Deze algoritmes leren relaties tussen inputkenmerken en numerieke uitkomsten.

🏠 Voorbeeld Voorspellen Van Huizenprijzen: Dit voorbeeld hebben we al een paar keer gezien, dus waarom niet nog eens gebruiken. Dit keer moet ons model meerdere factoren meenemen: grootte van het huis, kwaliteit van de locatie, aantal slaapkamers, leeftijd van het pand en lokale markttrends. Omdat we niet alle kenmerken willen uitschrijven (vooral als het er veel zijn), gebruiken we de notatie $1, ..., n$ . Dit betekent dat we beginnen bij 1 en eindigen bij $n$ , het laatste aantal dat we hebben. Onze formule blijft in hetzelfde format:

price = w_1 x_1 + w_2 x_2 + ... + w_n x_n + b

Laten we dit ontleden:

$x_1, x_2, ..., x_n$ vertegenwoordigen tot $n$ inputkenmerken (grootte, locatie, …).
$w_1, w_2, ..., w_n$ zijn gewichten die bepalen hoeveel elk kenmerk bijdraagt aan de prijs, $n$ komt overeen met het aantal inputkenmerken.
$b$ is de bias-term die een basisprijs geeft.

Tijdens training past het algoritme deze gewichten aan om voorspellingsfouten te minimaliseren over duizenden huizenverkopen. Met deze opzet krijgen we een voorspelde lijn:

Als we vervolgens een nieuw huis van 200m² op de markt brengen, kijken we gewoon naar de voorspelde lijn en zien dat de waarde ongeveer €125.000 kan zijn.

Het mooie van regression is de uitlegbaarheid—je ziet precies hoe elk kenmerk bijdraagt aan de uiteindelijke voorspelling. Als het gewicht voor locatie groot en positief is, betekent dat dat goede locaties huizenprijzen sterk verhogen.

Classification: Indelen In Categorieën

Classification-algoritmes voorspellen discrete categorieën of labels in plaats van continue getallen. De output is altijd één van een vooraf bepaalde set klassen.

📧 Voorbeeld Spamdetectie In E-mail: Wanneer je e-mailprovider een inkomend bericht analyseert, moet het beslissen: spam of legitiem? Dit heet een binair classificatieprobleem omdat er slechts twee mogelijke uitkomsten zijn.

Line plot showing training accuracy rising while validation accuracy falls over epochs

Image Creds

Het algoritme kijkt naar verschillende kenmerken van de e-mail—bepaalde sleutelwoorden, reputatie van de afzender, lengte van het bericht, aantal uitroeptekens—en combineert al deze informatie om een beslissing te nemen. In plaats van een simpel ja/nee-antwoord geven veel classification-algoritmes een betrouwbaarheidspercentage.

Classification is niet beperkt tot twee categorieën. Wanneer er meer klassen zijn, spreken we van Multi-class Classification. Een beeldherkenningssysteem kan foto’s bijvoorbeeld indelen in tientallen categorieën: kat, hond, auto, boom, persoon, enz. De principes blijven hetzelfde, maar het algoritme geeft waarschijnlijkheden voor elke mogelijke klasse.

Van Eenvoudige Naar Complexe Relaties

De lineaire modellen die we tot nu toe hebben gezien, zijn de eenvoudigste en meest uitlegbare benadering in machine learning. Ze gaan ervan uit dat relaties tussen inputs en outputs met rechte lijnen kunnen worden weergegeven.

👩🏻‍🏫 Voorbeeld Voorspellen Van Examenresultaten: Stel dat we de examenresultaten van studenten willen voorspellen op basis van studietijd. Als er een consistent verband is—meer studietijd leidt tot betere resultaten—kan lineaire regression dit patroon vastleggen:

\text{exam score} = w × \text{study hours} + b

Dit zou er erg vergelijkbaar uitzien met de plot die we eerder van lineaire regression zagen. Maar niet alle relaties zijn lineair—vaak hebben we complexere functies nodig.

Niet-Lineaire Relaties Modelleren

Relaties in de echte wereld zijn vaak geen rechte lijnen. Huizenprijzen kunnen langzaam stijgen voor kleine huizen, maar snel toenemen bij grotere huizen, wat een kromme relatie oplevert. Hier komt "Polynomial Regression" om de hoek kijken.

🏠 Voorbeeld Voorspellen Van Huizenprijzen: In plaats van een rechte lijn gebruiken we polynomial regression door hogere machten toe te voegen:

price = w_1 x + w_2 x^2 + w_3 x^3 + ... + b

Door kwadratische of kubieke termen toe te voegen, kan het model kromme patronen vastleggen. Deze fit past vaak beter bij huizenprijzen dan onze lineaire fit van eerder.

Het polynomial-model kan complexere patronen vastleggen, maar is ook gevoeliger voor overfitting—zeker met hogere machten.

Voorspellende Modellen: Leren Van Kansrekening

Terwijl regression relaties tussen numerieke variabelen modelleert, en classification data in categorieën verdeelt, gebruiken sommige modellen kansrekening. Deze modellen zijn bijzonder nuttig bij onzekerheid in data.

Naïve Bayes: Classificatie Door Kansrekening

Naive Bayes past de stelling van Bayes toe, waar we kort naar verwezen in Hoofdstuk 2, op classificatieproblemen. Ondanks de "naïeve" aanname dat alle kenmerken onafhankelijk zijn, werkt het verrassend goed.

Wiskundig stelt de stelling van Bayes:

P(class|features) = \frac{P(features|class)P(class)}{P(features)}

Laten we dit ontleden:

$P(\text{class} | \text{features})$ : kans op een bepaalde klasse gegeven de inputkenmerken.
$P(\text{features} | \text{class})$ : kans om die kenmerken te zien als de klasse bekend is.
$P(\text{class})$ : prior-kans dat die klasse voorkomt.
$P(\text{features})$ : algemene kans om die kenmerken te zien.

📧 Voorbeeld Spamdetectie: Stel dat een e-mail de zin “free money” bevat en van een onbekende afzender komt. Dan zouden de kansen er bijvoorbeeld zo uitzien:

$P(\text{spam}) = 0.3$ (30% van alle e-mails in de dataset is spam).
$P(\text{"free money"} | \text{spam}) = 0.8$ (“free money” komt voor in 80% van spamberichten).
$P(\text{unknown sender} | \text{spam}) = 0.6$ (60% van spamberichten komt van onbekende afzenders).

Het model combineert deze kansen tot een uiteindelijke beslissing:

P(class|features) = P(\text{"free money"} | \text{spam}) \cdot P(\text{unknown sender} | \text{spam}) \cdot P(spam)

Ondanks de vereenvoudigde aanname is Naive Bayes snel, effectief en veelgebruikt voor tekstclassificatie, medische diagnoses en sentimentanalyse.

Gradient Descent: Hoe AI Echt Leert

We hebben vaker gezegd dat modellen “gewichten aanpassen om fouten te minimaliseren,” maar hoe gebeurt dit? Het antwoord is gradient descent—een optimalisatietechniek die afgeleiden (uit Hoofdstuk 2) gebruikt om prestaties systematisch te verbeteren.

⛰ Voorbeeld Bergaf Lopen: Stel je voor dat je geblinddoekt op een heuvelachtig landschap staat en het laagste dal wilt bereiken. Gradient descent lijkt op steeds een stap nemen in de steilste neerwaartse richting. Uiteindelijk bereik je een dal—hopelijk het laagste.

Denk terug aan ons huizenprijs-model:

price = w_1 × size + w_2 × location + b

Gradient descent past de gewichten $w_1, w_2$ en bias $b$ aan door:

Fout berekenen: Hoe ver zitten we ernaast?
Gradient vinden: Afgeleiden gebruiken om te bepalen hoe we elk gewicht moeten aanpassen.
Stap nemen: Gewichten een beetje verplaatsen richting minder fout.
Herhalen: Totdat de fout niet verder daalt.

De learning rate bepaalt hoe groot de stappen zijn. Te groot en je springt heen en weer; te klein en het duurt eindeloos. Dit evenwicht is cruciaal in machine learning.

Clustering: Verborgen Groepen Vinden

In tegenstelling tot supervised algoritmes die leren van gelabelde voorbeelden, ontdekken clustering-algoritmes verborgen patronen in ongelabelde data.

K-Means Clustering: Een e-commercebedrijf wil zijn klantenbestand begrijpen zonder vooraf bepaalde categorieën. K-Means groepeert klanten op basis van koopgedrag:

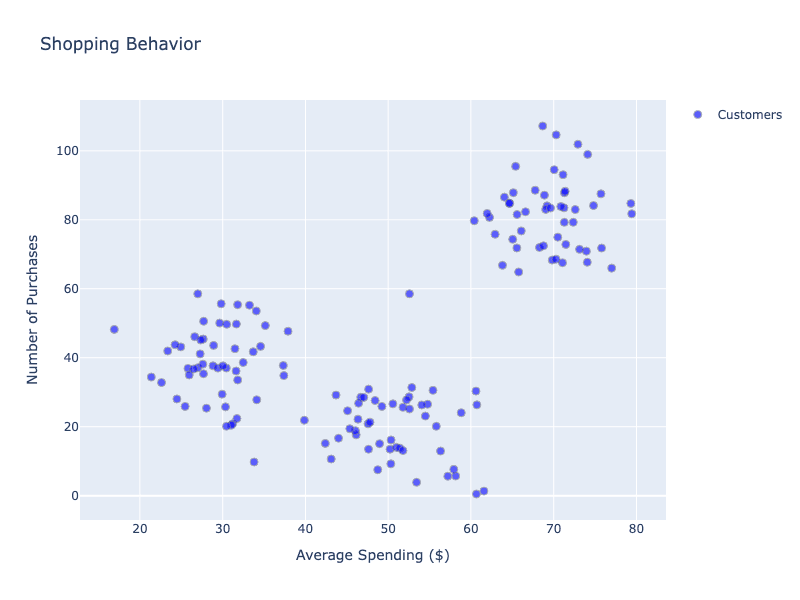
Na enkele iteraties ontstaan duidelijke groepen:

Budgetbewust: Lage uitgaven, hoge frequentie.
Premiumkopers: Hoge uitgaven, lage frequentie.
Incidentele Kopers: Gemiddelde uitgaven, onregelmatig patroon.

K-Means wordt veel toegepast, bijvoorbeeld voor marktsegmentatie of beeldsegmentatie in computer vision.

Dimensionality Reduction: Data Vereenvoudigen

Datasets uit de echte wereld hebben vaak te veel kenmerken om direct te analyseren of te visualiseren. Principal Component Analysis (PCA) reduceert deze complexiteit door data te projecteren op de richtingen met de meeste variatie—zoals het kiezen van de beste camerahoeken om de vorm van een 3D-object vast te leggen.

🫥 Voorbeeld Gezichtsherkenning: In plaats van elke pixel in een foto te analyseren (mogelijk duizenden kenmerken), identificeert PCA de belangrijkste variaties in gezichten—algemene vorm van het gezicht, positie van de ogen, structuur van de neus. Dit verlaagt de rekenbelasting terwijl de nauwkeurigheid behouden blijft.

Andere voordelen van Dimensionality Reduction:

Sneller trainen en voorspellen.
Minder opslagruimte.
Makkelijkere visualisatie.

Het reduceren van dimensies gaat altijd gepaard met enig informatieverlies. De sleutel is het vinden van de juiste balans tussen vereenvoudiging en het behouden van essentiële patronen.

De Juiste Algoritmes Kiezen

Dit hoofdstuk geeft een overzicht van technieken. Er bestaan echter veel meer varianten. De juiste keuze hangt af van:

Type Probleem:

Nummers voorspellen? Gebruik regression.
Data categoriseren? Gebruik classification.
Patronen vinden? Gebruik clustering of dimensionality reduction.

Eigenschappen Van De Data:

Kleine datasets: eenvoudige modellen zoals lineaire regression.
Grote datasets: complexere modellen.
Veel kenmerken: eerst dimensionality reduction overwegen.
Tekstdata: Naive Bayes is vaak een goed startpunt.

Behoefte Aan Uitlegbaarheid:

Beslissingen uitleggen? Lineaire modellen zijn duidelijk.
Black box acceptabel? Complexere modellen geven vaak hogere nauwkeurigheid.

De juiste techniek kiezen is een belangrijke stap in het bouwen van elk machine learning systeem.

Belangrijkste Inzichten

Machine learning-algoritmes vallen uiteen in duidelijke categorieën op basis van hun doel en aanpak. Regression voorspelt continue waarden, classification deelt data in categorieën en clustering vindt verborgen patronen. Elke benadering heeft zijn sterktes en ideale toepassingen. Door deze basis te begrijpen, kun je het juiste hulpmiddel kiezen voor elk machine learning-probleem dat je tegenkomt.

Kern Machine Learning-Algoritmes