Veelvoorkomende Uitdagingen

Het trainen van diepe neurale netwerken klinkt in theorie eenvoudig: definieer een netwerkarchitectuur, voer data in, draai backpropagation en gradient descent, en wacht op goede resultaten. In de praktijk is Deep Learning veel uitdagender. Netwerken kunnen memoriseren in plaats van leren, gradiënten kunnen verdwijnen of exploderen, en het vinden van de juiste hyperparameters vereist vaak uitgebreide experimenten.

Deze uitdagingen verklaren waarom deep learning nog steeds evenzeer kunst als wetenschap is, en waarom ervaren vakmensen intuïtie ontwikkelen door jaren van trial-and-error. Het begrijpen van deze veelvoorkomende valkuilen helpt te verklaren waarom het trainen van state-of-the-art-modellen weken of maanden kan duren, gespecialiseerde hardware vereist, en zorgvuldige monitoring tijdens het hele proces vraagt.

Overfitting: Wanneer Modellen Memoriseren In Plaats Van Leren

Overfitting is misschien wel het meest voorkomende probleem in deep learning. Het treedt op wanneer een model te gespecialiseerd raakt in zijn trainingsdata en specifieke voorbeelden leert in plaats van algemene patronen die overdragen naar nieuwe situaties.

🐱 Voorbeeld Katherkenning: Een netwerk dat traint op kattenfoto’s kan leren dat "afbeeldingen met bomen op de achtergrond katten zijn" als veel trainingsfoto’s toevallig katten bij bomen tonen. Wanneer het later een foto van een hond bij een boom tegenkomt, voorspelt het vol vertrouwen (en onjuist) "kat".

Wiskundig gezien gebeurt overfitting wanneer een model te veel capaciteit heeft ten opzichte van de hoeveelheid trainingsdata. Met miljoenen parameters kunnen diepe netwerken potentieel elk trainingsvoorbeeld memoriseren in plaats van onderliggende patronen te leren:

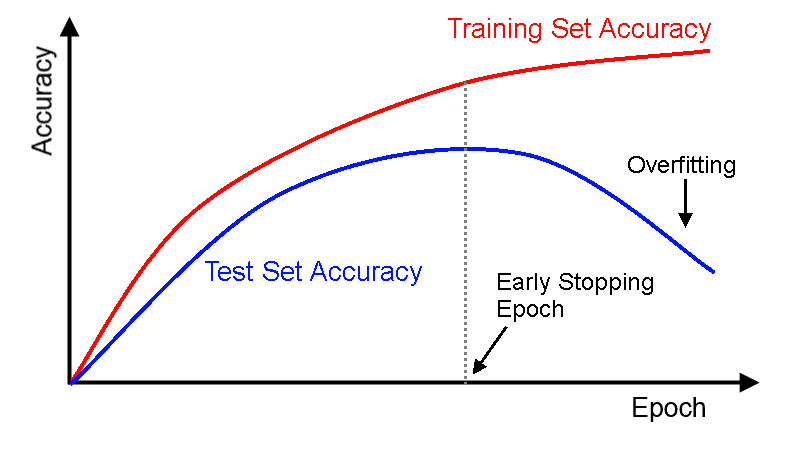
• Trainingsnauwkeurigheid blijft verbeteren terwijl validatienauwkeurigheid stagneert of daalt.
• Grote kloof tussen training- en validatieprestaties.
• Model doet zelfverzekerde voorspellingen op voorbeelden die sterk afwijken van de trainingsdata.

Oplossingen Voor Overfitting

Gelukkig zijn er technieken om overfitting te voorkomen.

Meer Data: De meest effectieve oplossing, hoewel vaak de duurste. Meer diverse trainingsvoorbeelden helpen modellen algemene patronen te leren in plaats van specifieke eigenaardigheden.

Regularisatie: Wiskundige technieken die modelcomplexiteit bestraffen. Bijvoorbeeld het stimuleren van spaarzame gewichten (veel gewichten worden nul), of kleine gewichten aanmoedigen, zodat geen enkele feature domineert.

Dropout: Tijdens training worden sommige neuronen in elke laag willekeurig "uitgeschakeld". Dit dwingt het netwerk om robuuste features te leren die niet afhankelijk zijn van specifieke neuronen—vergelijkbaar met hoe studeren met verschillende vriendengroepen je veelzijdiger maakt.

Vroege Stop (Early Stopping): Monitor de validatieprestatie en stop met trainen wanneer die begint te verslechteren, zelfs als de trainingprestatie blijft verbeteren.

Underfitting: Wanneer Modellen Te Simpel Zijn

Het tegenovergestelde probleem doet zich voor wanneer modellen onvoldoende capaciteit hebben om belangrijke patronen in de data vast te leggen. Dit is als proberen een kromme relatie te fitten met een rechte lijn—het model is fundamenteel te simpel voor de taak. Underfitting heeft enkele veelvoorkomende oorzaken:

• Onvoldoende modelcomplexiteit: Te weinig lagen of neuronen.
• Onvoldoende training: Stoppen voordat het model convergeert.
• Slechte learning rate: Te laag, waardoor effectieve gewichtsupdates uitblijven.
• Over-regularisatie: Zware straffen die leren verhinderen.

Net als bij overfitting kunnen we underfitting herkennen op verschillende manieren:

• Zowel training- als validatienauwkeurigheid blijven laag.
• Loss vlakt vroeg in de training af op een hoge waarde.
• Modelvoorspellingen lijken overdreven simplistisch of willekeurig.

Oplossingen Voor Underfitting

Underfitting kan worden aangepakt met enkele van deze technieken:

• Vergroot modelcapaciteit: Voeg lagen, neuronen of parameters toe.
• Train langer: Sta meer epochs toe voor convergentie.
• Hyperparameters aanpassen: Pas de learning rate aan.
• Feature-engineering: Bied betere inputrepresentaties.

Weet je nog de bias-variance trade-off uit Machine Learning? Overfitting en underfitting vertegenwoordigen de uiteinden van het bias-variance-spectrum. De kunst van deep learning ligt in het vinden van het optimale punt tussen deze extremen.

Het Loss-Landschap

Om te begrijpen waarom deep learning zo uitdagend is, moeten we visualiseren wat gradient descent daadwerkelijk probeert te bereiken. Het trainen van een neuraal netwerk betekent het vinden van de best mogelijke gewichten tussen miljarden mogelijkheden—als het vinden van het laagste punt in een uitgestrekt, complex landschap terwijl je geblinddoekt bent.

Het algoritme klinkt simpel: bereken gradiënten, zet stappen bergafwaarts, herhaal tot je de bodem bereikt. Dat is gemakkelijk voor simpele functies, zoals ons limonadekraamvoorbeeld terug in Hoofdstuk 2. Maar het "landschap" dat gradient descent in deep learning moet doorkruisen is buitengewoon complex. Bekijk deze representaties van loss-landschappen:

Uitdagende Terreinkenmerken

Echte loss-landschappen bestaan in ruimtes met miljoenen of miljarden dimensies, waardoor visualisatie en intuïtie uiterst lastig zijn. Dit brengt ook enkele moeilijke terreinkenmerken met zich mee:

Lokale Minima: Punten die vanuit de buurt optimaal lijken, maar niet het globale optimum zijn. Stel je een kleine vallei voor, omringd door heuvels, terwijl je niet weet dat er verderop een veel diepere vallei is.

Zadelpunten: Punten die in sommige richtingen dalen en in andere stijgen, zoals bergpassen. Deze kunnen gradient descent vastzetten omdat gradiënten bijna nul zijn, terwijl het geen echte minima zijn.

Plateaus: Vlakke gebieden waar gradiënten minuscuul zijn, waardoor leren dramatisch vertraagt. Het model kan duizenden iteraties doorbrengen met minimale vooruitgang.

Scherpe Kliffen: Gebieden waar gradiënten snel veranderen, wat kan leiden tot overshoot en instabiliteit in gradient descent.

Vanishing Gradients: Wanneer Diepe Netwerken Stoppen Met Leren

Naarmate netwerken dieper worden, verschijnt een fundamenteel wiskundig probleem: gradiënten kunnen exponentieel kleiner worden terwijl ze achterwaarts door lagen propagateren.

Tijdens backpropagation worden gradiënten berekend met de kettingregel, waarbij afgeleiden over lagen worden vermenigvuldigd. Wanneer activatiefuncties worden gebruikt, zijn deze afgeleiden vaak kleiner dan 1. Het vermenigvuldigen van veel kleine getallen produceert extreem kleine resultaten.

Bekijk het volgende voorbeeld van een gradiënt die achterwaarts stroomt:

• Laag 10: $\text{gradient} = 0.1$.
• Laag 9: $\text{gradient} = 0.1 × 0.3 = 0.03$.
• Laag 8: $\text{gradient} = 0.03 × 0.2 = 0.006$.
• Laag 7: $\text{gradient} = 0.006 × 0.4 = 0.0024$.
• ...
• Laag 1: $\text{gradient} ≈ 0.0000001$

Tegen de tijd dat gradiënten de vroege lagen bereiken, zijn ze zo klein dat gewichtsupdates verwaarloosbaar zijn. Dit kan grote gevolgen hebben:

• Vroege lagen leren zeer traag of stoppen helemaal met leren.
• Netwerken hebben extreem lang nodig om te trainen.
• Diepe architecturen presteren niet beter dan ondiepe.

Oplossingen Voor Vanishing Gradients

De Juiste Activatiefuncties Kiezen: ReLU heeft een afgeleide van 1 voor positieve inputs, wat gradiëntkrimp voorkomt.

Betere Gewichtsinitialisatie: Zorgvuldige initialisatie voorkomt vanaf het begin verdwijnende gradiënten. Bijvoorbeeld door gewichten te schalen op basis van laaggrootte of te starten op een gunstige positie voor je activatiefunctie.

Residual Connections: Skip-verbindingen laten gradiënten direct door lagen stromen en omzeilen potentiële verdwijnpunten. Dit is de sleutelinnovatie in ResNet-architecturen.

Batch Normalization: Normaliseert laaginvoer om een stabiele gradiëntstroom tijdens training te behouden.

Computationele En Praktische Uitdagingen

Naast wiskundige moeilijkheden kent deep learning aanzienlijke praktische obstakels, zoals:

Computationele Vereisten:

• Trainingstijd: State-of-the-art-modellen kunnen weken training vereisen op krachtige hardware.
• Geheugengebruik: Grote modellen passen mogelijk niet op standaard GPU’s en vragen gespecialiseerde infrastructuur.
• Energieverbruik: Het trainen van grote modellen kan evenveel elektriciteit verbruiken als een auto gedurende zijn levensduur.

Hardwareafhankelijkheden:

• GPU/TPU-vereisten: Het trainen van diepe netwerken op CPU’s is vaak onpraktisch.
• Geheugenlimieten: Grotere modellen vereisen duurdere hardware.
• Gedistribueerd trainen: Zeer grote modellen vereisen meerdere machines die samenwerken.

Deze praktische beperkingen onderstrepen dat vooruitgang in deep learning niet alleen afhangt van betere algoritmen, maar ook van de beschikbaarheid van krachtige en efficiënte hardware.

Waarom Deze Uitdagingen Ertoe Doen

Het begrijpen van deze moeilijkheden helpt verschillende belangrijke aspecten van moderne AI te verklaren.

• AI-onderzoek kost tijd; elke doorbraak vereist het overwinnen van fundamentele wiskundige en computationele obstakels, niet alleen algoritmische verbeteringen.
• Modellen zijn duur; de computationele vereisten voor het trainen en draaien van grote modellen creëren aanzienlijke infrastructuurkosten.
• Vooruitgang is incrementeel; elke verbetering in architecturen, optimalisatietechnieken of hardware maakt het mogelijk net iets complexere problemen op te lossen.

Het erkennen van deze uitdagingen benadrukt waarom vooruitgang in deep learning moeizaam wordt geboekt en waarom elke stap vooruit een belangrijke prestatie in AI vertegenwoordigt.

Belangrijkste Inzichten

Het trainen van diepe neurale netwerken houdt in dat je wiskundige, computationele en praktische uitdagingen moet navigeren. Overfitting en underfitting weerspiegelen de trade-off tussen modelcomplexiteit en generalisatie. Het loss-landschap zit vol lokale minima, zadelpunten en plateaus die gradient descent kunnen vastzetten of vertragen. Vanishing en exploderende gradiënten compliceren diepere architecturen, wat oplossingen vereist zoals ReLU-activaties, zorgvuldige initialisatie en nieuwe netwerkontwerpen.

Daarbovenop maken grote computationele vereisten en hyperparametergevoeligheid training zowel kostbaar als veeleisend. Deze obstakels verklaren waarom succes in deep learning niet alleen op theorie berust, maar ook op praktische ervaring, middelen en volharding—en waarom elke doorbraak een moeizaam behaalde vooruitgang vertegenwoordigt.