The Perceptron

Before diving into complex neural networks, we need to understand their most basic component: the perceptron. Think of it as the brick of Deep Learning (DL)—individually simple, but when combined in clever ways, capable of building incredibly sophisticated systems.

The perceptron was invented in 1957 and represents one of the first attempts to mimic how brain neurons work. While a single perceptron is limited, understanding how it processes information and learns from mistakes gives you the foundation for grasping modern AI systems like ChatGPT and image recognition networks.

What is a Perceptron?

A perceptron is inspired by biological neurons in your brain. Just like a neuron receives signals from other neurons and "fires" if the combined signal is strong enough, a perceptron receives numerical inputs, processes them, and produces a simple yes or no decision.

A perceptron implements a specific type of function:

You should be able to recognize much of this formula, but let's break down the components:

• $x_1, x_2, ..., x_n$ are iput values (like features we learned about in Machine Learning).
• $w_1, w_2, ..., w_n$ are weights (the importance of each input).
• $b$ is again the bias term.
• $y$ represents the output (1 for "yes", 0 for "no").

The process is as follows:

1. Take each input and multiply it by its corresponding weight.
2. Add all these weighted inputs together.
3. Add the bias term.
4. If the total is positive, output 1; if negative or zero, output 0.

Take a look at the diagram below:

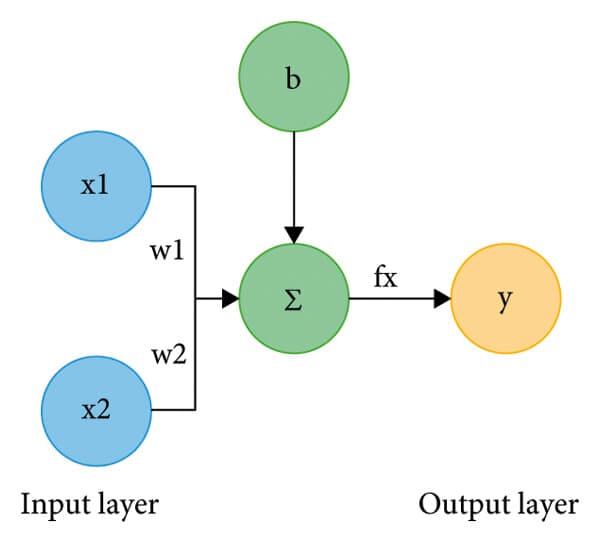
Each input is multiplied by a weight, the results are summed (denoted by $\sum$), and the perceptron decides whether the total is high enough to “fire”.

A Practical Example: Should You Go Running?

Let's make this concrete with a decision you might face: whether to go for a run. Let's say we have gathered the following data that might be relevant:

• Weather quality (0-10): $x_1 = 8$ (nice day).
• Available time (hours): $x_2 = 1.5$ (some time available).
• Energy level (0-10): $x_3 = 6$ (moderately energetic).

Through experience, you've learned that:

• $w_1 = 0.3$ (weather matters, but not everything).
• $w_2 = 0.8$ (time is very important).
• $w_3 = 0.4$ (energy level matters moderately).
• $b = -3$ (you generally prefer staying inside, so need convincing).

Using the logic of the perceptron we can make a calculation:

Since $3.0 \gt 0$, the perceptron outputs 1 so let's go for a run!

This demonstrates how the perceptron weighs different factors and makes a binary decision based on the combined evidence.

Learning Through Examples

Let's see how a perceptron learns to make better predictions over time using another example. We predict whether a student will pass an exam based on:

1. Hours studied ($x_1$).
2. Hours slept the night before ($x_2$).

We assign weights (randomly), remember each feature $x_i$ has it's own weight $w_i$:

• $w_1 = 0.6$.
• $w_2 = 0.4$.
• Let's not forget the bias $b = -0.5$.

We can test our initial model, if a student studied for 3 hours and slept for 5:

Since $3.3 \gt 0$ the perceptron returns 1 and the student passes. If the student actually passed, our prediction was correct! But if they failed, we need to adjust our weights.

When the perceptron makes a mistake, it adjusts weights in the direction that would have made the correct prediction. This is similar to the gradient descent concept we learned in Chapter 3, but simpler.

• If we predicted "pass" but student failed → reduce weights that contributed to the high score.
• If we predicted "fail" but student passed → increase weights that should have contributed more.

Over many examples, the perceptron finds weights that minimize mistakes—just like the optimization process we saw in machine learning!

What Perceptrons Can and Cannot Do

Perceptrons are powerful for certain types of problems but have important limitations. They are good at:

• Linear classification: Problems where you can draw a straight line to separate categories.
• AND/OR logic: Simple logical operations.
• Binary decisions: Any yes/no classification with linearly separable data.

😈 The XOR Problem: The classic limitation of perceptrons is the XOR (exclusive or) problem, take the following data points:

• (0,0) → circle
• (0,1) → star
• (1,0) → star
• (1,1) → circle

Take some time to think about how they would look in a grid. How can we separate classes "star" and "circle" with a straight line?

No single straight line can separate the stars from the circles in this pattern. This limitation drove researchers to develop multi-layer networks, which we'll explore next.

Some real-world limitations the perceptron faces:

• Image recognition: A single perceptron can't recognize complex visual patterns
• Language understanding: Sentence meaning involves non-linear relationships between words
• Complex decision-making: Most real-world problems require considering interactions between features

In short, while perceptrons introduced the foundations of neural networks, their limitations highlight why deeper architectures are essential for solving complex, real-world problems.

Historical Significance

The perceptron, invented by Frank Rosenblatt in 1957, was one of the first machine learning algorithms that could learn from data. Early demonstrations showed perceptrons learning to recognize simple patterns, generating enormous excitement about artificial intelligence.

However, when researchers proved that perceptrons couldn't solve problems like XOR, interest in neural networks declined for decades. This period, known as the "AI Winter," lasted until researchers figured out how to train multi-layer networks effectively.

Today, the perceptron remains the fundamental building block of modern deep learning. Every neuron in ChatGPT, image recognition systems, and other AI applications is essentially a more sophisticated version of the original perceptron concept.

Connection to Modern AI

While simple, perceptrons introduced several concepts that remain central to modern AI:

Weight Learning: The idea that AI systems should learn appropriate feature weights from data rather than having them hand-coded.

Threshold Decisions: The concept of combining multiple inputs to make binary decisions, though modern systems use more sophisticated activation functions.

Iterative Improvement: The principle that AI systems improve through repeated exposure to training examples and error correction.

Understanding perceptrons helps you appreciate that even the most advanced AI systems are built from relatively simple mathematical operations, repeated millions or billions of times.

Final Takeaways

The perceptron represents the fundamental unit of computation in neural networks—a simple mathematical function that weights inputs and makes binary decisions. While limited to linearly separable problems, perceptrons introduced the key principles of learning from data through weight adjustment and iterative error correction. Their historical significance lies not just in their capabilities, but in demonstrating that machines could learn to make decisions from examples rather than explicit programming.

Understanding perceptrons provides the conceptual foundation for grasping how complex modern AI systems work, as they're essentially sophisticated networks of interconnected perceptron-like units working together to solve complex problems.